Обработка данных эксперимента в программе EXCEL

Пусть был проведен, например, эксперимент, позволяющий выявить влияние температуры на количество потребляемого корма семьей пчел во время зимовки (таб. 1).

Таблица  1

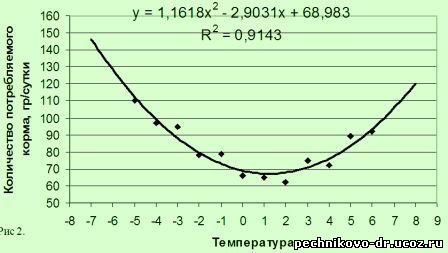
После получения экспериментальных данных их необходимо обработать соответствующим образом. Так полученные здесь результаты можно представить в виде точечного графика (рис 1), который передает их более наглядно по сравнению с таблицей. Не стоит спешить соединять точки графика ломаной линией. В этом случае никакой зависимости не получится по той причине, что экспериментально полученные данные во первых никогда не бывают абсолютно точными из-за погрешностей измерительных инструментов, неточностей снятия показаний и т.п. Кроме того, может оказаться так, что данный фактор вообще не влияет на изменение характеристик объекта, или влияет достаточно слабо, уступая место другим, более значащим факторам. Выявить степень влияния фактора на объект позволяет корреляционный анализ. Но он сложен и его не стоит рекомендовать для массового использования в курсе школы. Исключением может стать случай линейной зависимости между рядами данных. В этом случае коэффициент корреляции может быть рассчитан с использованием компьютерной программы «Excel» см. ниже. Часто, для того, что бы установить факт влияния фактора на объект, достаточно взглянуть на расположение точек на графике зависимости характеристики объекта от фактора. Так на приведенном точечном графике (рис 1) сразу заметно, что точки располагаются не хаотично, а создают образ некой кривой, что говорит о существовании взаимосвязи.

Следующим шагом в обработке данных станет построение регрессионной модели. Такая модель (математическая функция) строится в два этапа. На первом этапе выбирается вид функции, а на втором этапе производится вычисление параметров выбранной функции. Чаще всего выбор производится из следующих функций:

 y = ax + b   - линейная функция;

 y = ax² + bx + c  - квадратичная функция (полином второй степени);

 y = ax³ + bx² + cх + d  -  полином третей степени (так же используются полиномы и более высоких степеней)

y = aln(x) + b  - логарифмическая функция;

y = ae^bx – экспоненциальная функция;

y = ax^b  - степенная функция.

 Во всех этих формулах  х – аргумент, y – значение функции, a,b,c,d – параметры функций. Ln(x) – натуральный логарифм, e – константа, основание натурального логарифма.

Содержание.

1.      Построение регрессионной модели.

2.      Создание вариационного ряда, вариационной кривой, определение среднего значения и среднеквадратичного отклонения.

3.      Доверительная вероятность.

4.      Корреляционный анализ.

5.     Поиск оптимума.